编译原理复习

选择题

存储分配

C 语言和 Pascal 语言属于动态栈式存储分配

Python 属于静态存储分配

算符匹配

若 α ∈ first（α），α ∉ first（β），那么α用α还是β推导？

💡显然是用 α 进行推导。用 β 产生不了 α ，会产生回溯，根本无法完成推导

后缀表达式

例如：9+ ( 3 - 1) * 3 + 10 / 2 (四则表达式形式)

先做：(3 - 1) = 2

其次： 2 * 3 = 6

接着：10 / 2 = 5

接着：9 + 6 = 15

接着：15 + 5 = 20

写成后缀表达式：9 3 1 - 3 * + 10 2 / +

运算顺序

💡 规则
当是数字时，从左至右依次入栈
当是运算符时，从栈顶拿两个元素进行运算，再将结果入栈

例题1：8 + 4 - 6 * 2用后缀表达式表示为 8 4 + 6 2 * 1

例题2：2 * (3 + 5) +7 / 1 - 4用后缀表达式表示为 2 3 5 + * 7 1 / + 4 -

终态与初态的判定

终态 S → S·

初态 S → ·S

优先关系判断

对于P→…Rb… ,R的尾终结符是α(R→…a 或 R→…aQ)

则a和b的优先关系是 a > b

💡始终是非终结符优先

简答题

证明二义文法

例题：证明 E→E + E | E * E | ( E ) | i 为二义文法

💡举出一个反例

解：对于句子(i * i + i)

E → ( E ) → (E + E) → (E * E + E) →(i * E + E) → (i * i + i)
E → ( E ) → (E * E) → (i * E) → (i * E + E) → (i *i + E) → (i * i + i)

此句型有两颗不同的语法树，所以为二义文法！

语法树

💡补充：证明xxx不是LR文法 = 证明xxx是二义文法 + 任意二义文法都不是LR文法

DFA的构造1

例题：构造一个DFA，使他识别{0, 1}上以00结尾的字符串

解：正规表达式：( 0 | 1 )* 0 0

根据题意构造NFA（从终态出发）

NFA

状态/读入	0	1
I0 = {S}	I1 = {S, A}	I0 = {S}
I1 = {S, A}	I2 = {S, A, Z}	I0 = {S}
I2 = {S, A, Z}	I2 = {S, A, Z}	I0 = {S}

构造DFA，如图所示

💡期末变形版：构造一个DFA，使他识别{a, b}上以aa结尾的字符串

DFA的构造2

例题：构造一个（最小化）DFA，使它识别{0，1}上至少含有两个连续的1的字符串

解：正规式 (0 | 1)* 1 1 (0 | 1)*

正规文法

A→0A | 1A | 1B

B→1C | 1

C→0C | 1C | 0 | 1

NFA

NFA转DFA

状态/读入	0	1
I0 = {A}	I0 = {A}	I1 = {A, B}
I1 = {A, B}	I0 = {A}	I2 = {A, B, C}
I2 = {A, B, C}	I3 = {A, C}	I2 = {A, B, C}
I3 = {A, C}	I3 = {A, C}	I2 = {A, B, C}

💡Tips：可以分别求出A，B，C读入0或者1的值，然后按需求取并集

状态/读入	0	1
A	A	A,B
B	/	C
C	C	C

DFA(未最小化)

递归下降分析程序

例题：写出下列文法中S和B的递归下降分析程序

S→id = E | if ( E ) S B | while ( E ) S | do S while ( E )

B→ else S | ε

void S() {
    if (sym == "id") {
        read();
        if (sym == "=") {
            //read() 表示 sym<-读单词
            read();
            E();
        } else
            error();
    } else if (sym == "if") {
        read();
        if (sym == "(") {
            read();
            E();
            if (sym == ")")
                read();
            else
                error();

        } else
            error();
        S();
        B();
    } else if (sym == "while") {
        read();
        if (sym == "(") {
            read();
            E();
            if (sym == ")")
                read();
            else
                error();
        } else
            error();
        S();
    } else if (sym == "do") {
        read();
        S();
        if (sym == "while") {
            read();
            if (sym == "(") {
                read();
                E();
                if (sym == ")")
                    read();
                else
                    error();
            } else
                error();
        } else
            error();
    }
}

void B() {
    if (sym == "else") {
        read();
        S();
    }
    else if (sym == "ε") {
        read();
    }
    else
        error();
}

LL(1)分析表

例题：文法G：(1)A→aAB1 | a (2)B→Bb | d

(1)消去左递归并提取公因子

解：

A→aA’ A’→AB1 | ε

B→dB’ B’→bB’ | ε

(2)构造该文法的LL(1)分析表

解：分别求出First、Follow集

First(A)={a}

First(A)

First(A’)=First(A)∪{ε}={a, ε}

First(A’)

First(B)={d}

First(B)

First(B’)={b, ε}

First(B’)

补充：事后发现这里有一点问题，因为A是文法开始符号，所以#∈Follow(A)

而Follow(A)∈Follow(A’)，所以把#加入到Follow(A’)。

~~而不是像图片中那样胡说~~

Follow(A)

💡B能跟在A后面，所以B的终结首符可以是A的随符

Follow(B) = Follow(B') = {1}

算符优先分析表

例题：下列文法G

S’→#S#

S→D(R)

R→R ; P | P

P →S | i

D→i

(1)写出文法G中每个非终结符的FIRSTVT集和LASTVT集；

(2)构造文法G的算符优先分析表;

FIRSTVT集

将文法进一步拆分

S’→#S#	S→D(R)	R→R ; P	R→P
P→S	P→i	D→i

💡反复使用下面两条规则构造集合FIRSTVT(P)
若有产生式P→a…或P→Qa… ，则a∈FIRSTVT(P)
若a∈FIRSTVT(Q)，且有产生式P→Q…，则a∈FIRSTVT(P)

下面首先使用规则1

	#	(	)	;	i
S'
S
R
P
D

先看 S’这一行，关于S’的产生式，只有S’→#S# (符合P→a…)

所以（S’, #) = √

	#	(	)	;	i
S'	✔
S
R
P
D

S这一行，关于S的产生式，只有S→D(R) (符合P→Qa…)

所以（S, ( ) = √

	#	(
S'	✔
S		✔
R
P
D

R这一行，关于R的产生式有R→R ; P（符合P→Qa…），R→P（不符合）

所以（R, ; ) = √

	#	(	;
S'	✔
S		✔
R			✔
P
D

P这一行，关于P的产生式有P→S（不符合），P→i（符合P→a…）

所以（P, i ) = √

	#	(	;	i
S'	✔
S		✔
R			✔
P				✔
D

D这一行，关于D的产生式有D→i（符合P→a…）

所以（D, i ) = √

	#	(	;	i
S'	✔
S		✔
R			✔
P				✔
D				✔

接下来使用规则2

💡找产生式右边第一个是非终结符的式子

我们可以发现这几个符合题意

S→D(R)

R→R ; P

R→P

P→S

💡利用规则2：对于P→Q…，将FIRSTVT(Q)赋给FIRSTVT(P)

那么在下面的式子中，我们这样赋值

FIRSTVT(D)→FIRSTVT(S)
FIRSTVT(R)→FIRSTVT(R) //忽略
FIRSTVT(P)→FIRSTVT(R)
FIRSTVT(S)→FIRSTVT(P)

整理一下顺序 D→S→P→R（顺序千万不能错！）

D→S S→P P→R

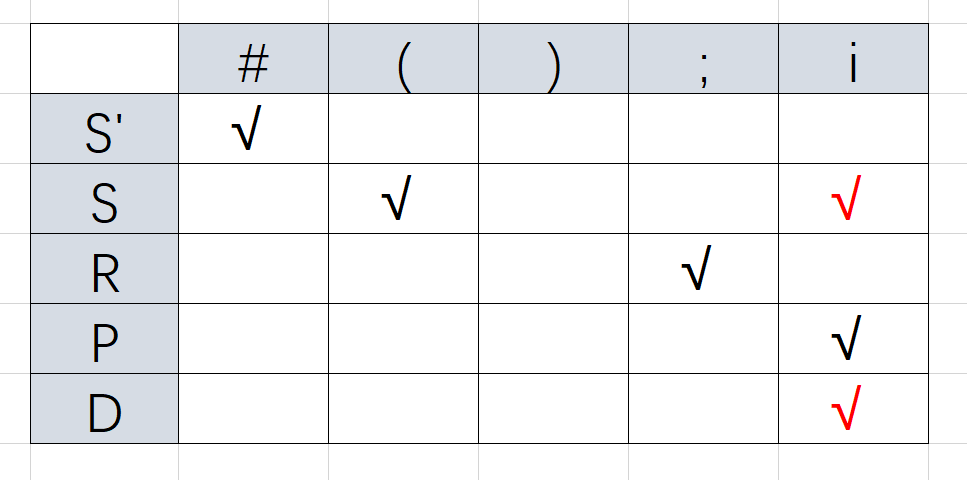
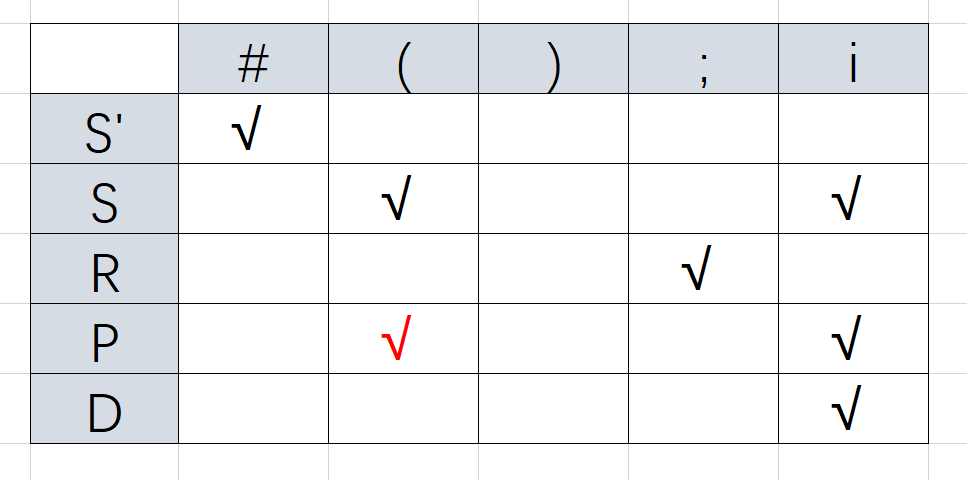
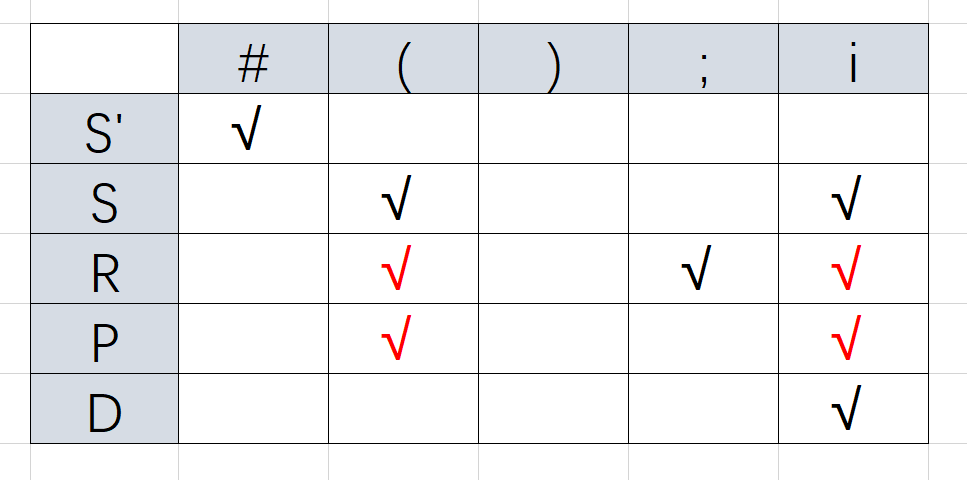
最终得到FIRSTVT集

	#	(	;	i
S'	✔
S		✔		✔
R		✔	✔	✔
P		✔		✔
D				✔

LASTVT集

💡反复使用下面两条规则构造集合LASTVT(P)
若有产生式 P→…a 或 P→…aQ，则 a ∈ LASTVT(P)
若a∈LASTVT(Q)，且有产生式 P→…Q，则 a ∈ LASTVT(P)

方法应该和上面类似，我就不详细展开了

最终得到LASTVT集

	#	)	;	i
S'	✔
S		✔
R		✔	✔	✔
P		✔		✔
D				✔

算符优先分析表

💡利用以下规则构造算符优先分析表
同一个产生式中有两个非终结符，两者优先关系相等
对于P→aQ（非终结符在前）：a<FIRSTVT(Q) 横着填
对于P→Qa（非终结符在后）：LASTVT(Q)>a 竖着填

举个例子，对于 S’→#S#，从左往右依次扫描：

我们首先发现：# 和 # 优先关系相等

进一步拆分：

拆分	结果
# S	#<FIRSTVT(S)
S #	LASTVT(S)>#

	(	i	#
(
)			>
;
i
#	<	<	=

依次扫描每一个表达式，最终完成构造

	(	)	;	i	#
(	<	=	<	<
)		>	>		>
;	<	>	>	<
i	>	>	>
#	<			<	=

语义子程序

布尔表达式

(1) E → i{
    E.TC=NXQ;
    E.FC=NXQ+1;
    GEN(jnz,ENTRY(i), _ , 0);
    GEN(j, _ , _ , 0);
}

(2) E → E(1)rop E(2){
    E.TC=NXQ;	
    E.FC=NXQ+1;
    GEN(jrop, E(1).PLACE, E(2).PLACE , 0);
    GEN(j, _ , _ , 0);
}

(3) E → (E(1)){
    E.TC=E(1).TC;
    E.FC=E(1).FC;
}

(4) E → ┐E(1){
    E.TC=E(1).FC;
    E.FC=E(1).TC;
}

(5) EA → E(1)^{	
    backpatch(E(1).TC,NXQ);
    EA.FC=E(1).FC;
}

(6) E → EAE(2){
    E.TC=E(2).TC;
    E.FC=merg(EA.FC, E(2).FC)
}

(7) E0 → E(1)∨{
    backpatch(E(1).FC,NXQ);
    E0.TC=E(1).TC;
}

(8) E → E0E(2){
    E.FC=E(2).FC;
    E.TC=merg(E0.TC, E(2).TC)
}

if语句

(1) C →if (E) {
    backpatch(E.TC,NXQ);
    C.CHAIN=E.FC;
}

(2) S →C S1{
    S.CHAIN=merg(C.CHAIN,S1.CHAIN);
}

(3) T →C S1 else {
    q=NXQ;GEN(j, _ , _ , 0);
    backpatch(C.CHAIN,NXQ);
    T.CHAIN=merg(S1.CHAIN,q);
}

(4) S →T S2 {
    S.CHAIN=merg(T.CHAIN,S2.CHAIN)
 }

四元式和汇编代码

这里主要考察if嵌套if或者while嵌套if

源程序

if嵌套if

if (a)
	if (b)
	    A=2;
	else
	    A=3;
else if (c)
	A=4;
else
	A=5;

四元式

(1): (jnz,a,-,3)
(2): (j,-,-,9)
(3): (jnz,b,-,5)
(4): (j,-,-,7)
(5): (=,2,-,A)
(6): (j,-,-,14)
(7): (=,3,-,A)
(8): (j,-,-,14)
(9): (jnz,c,-,11)
(10): (j,-,-,13)
(11): (=,4,-,A)
(12): (j,-,-,14)
(13): (=,5,-,A)

汇编代码

DATAS SEGMENT
    a DW 0
    b DW 0
    c DW 0
    A DW 0
DATAS ENDS

STACKS SEGMENT

STACKS ENDS

CODES SEGMENT
    ASSUME CS:CODES,DS:DATAS,SS:STACKS
START:
    MOV AX,DATAS
    MOV DS,AX
    MOV DX,0
    CMP a,0
    JNZ L1
    JMP L4
L1: CMP b,0
    JNZ L2
    JMP L3
L2: MOV AX,2
    MOV A,AX
    JMP L7
L3: MOV AX,3
    MOV A,AX
    JMP L7
L4: CMP c,0
    JNZ L5
    JMP L6
L5: MOV AX,4
    MOV A,AX
    JMP L7
L6: MOV AX,5
    MOV A,AX
L7: MOV AH,4CH
    INT 21H
    CODES ENDS
END START

while嵌套if

源程序

    int a, b, d, x, y;
    while (a||b < d)
        if (x > 6 + 3)
            x = x - 2 * 3;
        else
            y = x + 3 * 4;

四元式

(1): (jnz,a,-,5)
(2): (j,-,-,3)
(3): (j<,b,d,5)
(4): (j,-,-,15)
(5): (j>,x,6,7)
(6): (j,-,-,11)
(7): (*,2,3,T1)
(8): (-,x,T1,T2)
(9): (=,T2,-,x)
(10): (j,-,-,14)
(11): (*,3,4,T3)
(12): (+,x,T3,T4)
(13): (=,T4,-,y)
(14): (j,-,-,1)

汇编代码

DATAS SEGMENT
    a DW 0
    b DW 0
    d DW 0
    x DW 0
    y DW 0
    T1 DW 0
    T2 DW 0
    T3 DW 0
    T4 DW 0
DATAS ENDS

STACKS SEGMENT

STACKS ENDS

CODES SEGMENT
    ASSUME CS:CODES,DS:DATAS,SS:STACKS
START:
    MOV AX,DATAS
    MOV DS,AX
    MOV DX,0
L1: CMP a,0
    JNZ L3
    JMP L2
L2: MOV BX,d
    CMP b,BX
    JB L3
    JMP L7
L3: CMP x,6
    JA L4
    JMP L5
L4: MOV AX,2
    MOV DI,3
    MUL DI
    MOV T1,AX
    MOV BX,x
    MOV AX,T1
    SUB BX,AX
    MOV T2,BX
    MOV AX,T2
    MOV x,AX
    JMP L6
L5: MOV AX,3
    MOV DI,4
    MUL DI
    MOV T3,AX
    MOV AX,x
    MOV BX,T3
    ADD BX,AX
    MOV T4,BX
    MOV AX,T4
    MOV y,AX
L6: JMP L1
L7: MOV AH,4CH
    INT 21H
    CODES ENDS
END START

简单说一下分析过程：

首先jnz具体跳转到一行代码我们是不知道的，但是我们知道跳转到哪一条语句

于是第一轮我们这样写

(jnz，a，_，判断b)
(j，_，_，判断c)
判断b：(jnz，b，_，赋值A=2)
(j，_，_，赋值A=3)
赋值A=2：(=，2，_，A)
(j，_，_，结束)
(=，3，_，A)
(j，_，_，结束)
(jnz，c，_，赋值A=4)
(j，_，_，赋值A=5)
赋值A=4：(=，4，_，A)
赋值A=4：(j，_，_，结束)
(=，5，_，A)
结束：

然后我们在每一行前面加上序号

(1) (jnz，a，_，判断b)
(2) (j，_，_，判断c)
(3) 判断b：(jnz，b，_，赋值A=2)
(4) (j，_，_，赋值A=3)
(5) 赋值A=2：(=，2，_，A)
(6) (j，_，_，结束)
(7) (=，3，_，A)
(8) (j，_，_，结束)
(9) (jnz，c，_，赋值A=4)
(10) (j，_，_，赋值A=5)
(11) 赋值A=4：(=，4，_，A)
(12) 赋值A=4：(j，_，_，结束)
(13) (=，5，_，A)
(14) 结束：

最后把相应的中文语句换成前面对应的序号就可以了~